这个页面可能对大多数读者没有兴趣。它包含了一些对卢卡斯-彭罗斯关于哥德尔定理的论证的草稿回应。在我写完这些之后,我发现我对这个论证应该如何运作更加困惑了,所以我不再认为这些观点是恰当的。
我的第一个回应
注意:我对以下主题理解不深,所以我下面说的可能是错误的。阅读时请自行判断。
卢卡斯-彭罗斯关于哥德尔定理的论证可能是在认知科学上误导人的欺骗性数学的典型例子。已经有许多回应被提出,我在这里不会复述。我将提出我个人对这个困惑的看法。
考虑彭罗斯的哥德尔论证:
(1) 假设"我的推理能力被某个形式系统F所捕获",并且基于这个假设,"考虑我能知道为真的陈述类"。(2) 由于我知道我是可靠的,F是可靠的,所以F'也是可靠的,F'只是F加上(1)中做出的假设,即我是F(顺便说一下,可靠的形式系统是指只有有效论证才能被证明的系统)。但是(3)"我知道G(F')是真的,其中这是系统F'的哥德尔句子"(同上)。然而,(4)哥德尔第一不完备性定理表明F'无法看到哥德尔句子是真的。此外,我们可以推断(5)我就是F'(因为F'只是F加上(1)中做出的假设,即我是F),我们也可以推断我能看到哥德尔句子的真实性(因此既然我们是F',F'能看到哥德尔句子的真实性)。也就是说,(6)我们得到了一个矛盾(F'既能看到哥德尔句子的真实性,又不能看到哥德尔句子的真实性)。因此,(7)我们的初始假设必须是错误的,也就是说,F或任何形式系统都无法捕获我的推理能力。
作为一个计算主义者,我同意(1)——至少如果所考虑的"形式系统"足够面向物理,能够潜在地包括基于物理定律对物理大脑状态的操作。根据物理丘奇-图灵论题,这些物理操作原则上可以在图灵机上以足够的精度模拟,即一个形式系统。
许多批评者反对(2),我可能也反对,但我认为这不是根本错误所在,所以让我们也给彭罗斯(2)。
我反对(3)。我"知道"G(F')为真的大脑状态是一种状态,在这种状态下,我正在对F'的一些大概念云泡进行抽象操作,记住哥德尔句子是如何工作的,并意识到类似的趋势在这里适用,这将使G(F')为真。这是高层次的、启发式的、模式匹配推理。我大脑在做这件事时的状态是F'的某个"定理",但它不是对应于形式证明F'的定理。那将是一个复杂得多的物理状态。F'无法看到G(F')真实性的意义是在后者这种严格形式的意义上,而我的大脑在以非正式方式直观地理解G(F')的真实性时并没有达到这种状态。因此,哥德尔第一不完备性定理与我对G(F')的直观把握无关。
John Baez在不同的背景下解释了这个想法,我将其应用到彭罗斯的情况:
现在发生的是[彭罗斯]在直观意义上使用"可证明",其中任何完全令人信服的论证都算作证明。[...]
但在形式逻辑中,我们必须写下一套精确的证明规则;然后我们说某事是"可证明的",如果它是使用这些规则可证明的。
基本上,彭罗斯混淆了
- 在F'内证明G(F'),根据哥德尔定理,人类显然无法做到这一点
- 达到一种不同于G(F')完整形式证明的状态,这种状态对应于我们的大脑使用启发式模式匹配推理(可能是正确的)直观地理解G(F')的真实性。
如果可能的话,在F'内证明G(F')将涉及一系列极其复杂的步骤,这与人类在看到G(F')为真时所做的完全不同。当然,彭罗斯同意这一点,但他忘记了F'的某些其他形式操作结果可以是人类直观理解G(F')为真的状态。
彭罗斯应该问:如果人类不正式证明G(F'),他们是如何做到的?如果计算主义者是正确的,人类使用的任何物理过程都可以被建模为形式系统上的操作。但这些操作不需要与证明他们直观把握的同一定理的操作序列有任何相似之处。
为了再次强调这一点,这里是一个总结图:
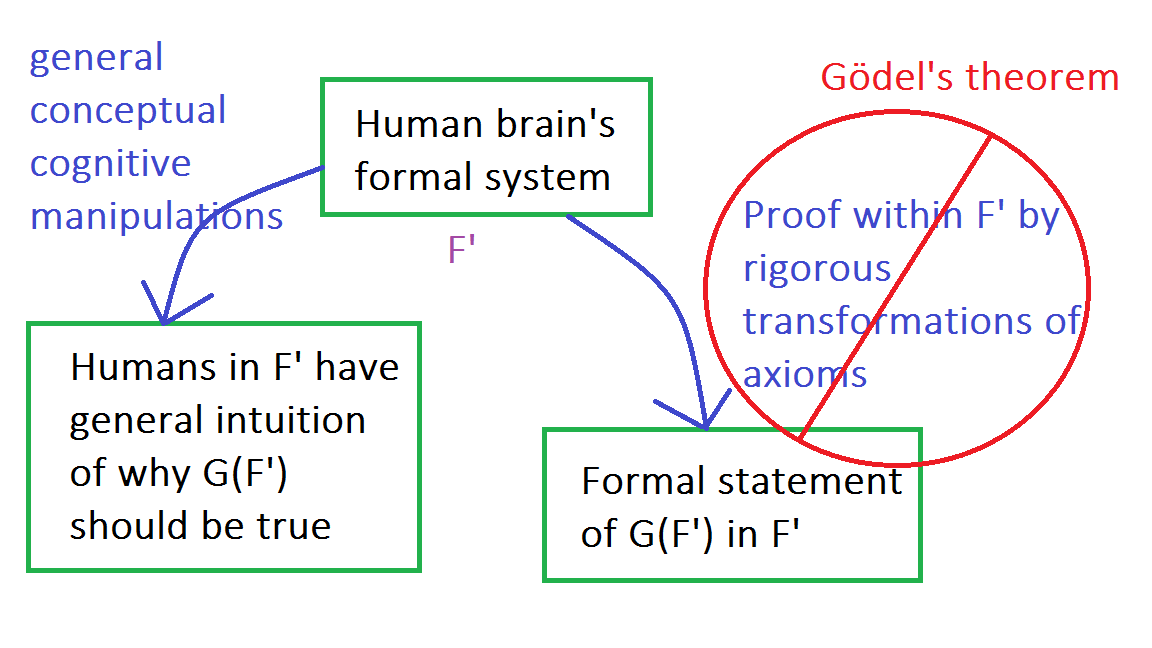
我的第二个回应
在"心智、机器和哥德尔"(1961)中,John R. Lucas解释了如何将机器转换为形式系统:系统的初始条件可以被视为公理,从一个系统状态转换到另一个系统状态的规则可以被视为if-then推理规则。随着机器向前推进,其形式系统对应物将系统地"证明"新定理,机器的每个新状态都是一个新定理。
Lucas没有提供实际例子,但让我试一试。让一个人的初始状态由描述他的所有物理变量以足够精度指定。然后这个物理系统以推理规则演化,如"如果这个人处于状态#02934234823472938439439(原子#1位于位置(.2034,2.342,99.204),原子#2位于位置...,原子#1的速度是...,等等),那么这个人移动到状态#82342398423492384392423(原子#1位于位置...,原子#1的速度是...,等等)。"从人的初始状态这个唯一公理开始,这个系统将为系统的每一个下一步推导出一个新的"定理"(状态)。如果系统回到早期状态,那么它将证明的定理就不会是新的,但在人的一生中,一个人似乎不太可能回到他之前的某个物理状态。
事实上,上述规范似乎不够充分,因为人类系统的推理规则没有环境输入的知识就无法工作。而且没有更广泛环境的知识,无法完美预测局部环境的行为。所以与其将一个离散的人建模为一台机器,我认为我们应该将整个宇宙建模为一台机器,或者至少是宇宙的某个独立子系统,其演化不依赖于外部事件。换句话说,Lucas的论证已经从试图用计算主义反驳心智,转向试图反驳整个宇宙的计算主义,因为心智无法与宇宙隔离。
Roger Penrose发展了Lucas论证的其余部分的一个变体,我将在这里关注它。我引用互联网哲学百科全书条目中的摘要:
(1) 假设"我的推理能力被某个形式系统F所捕获",并且基于这个假设,"考虑我能知道为真的陈述类"。(2) 由于我知道我是可靠的,F是可靠的,所以F'也是可靠的,F'只是F加上(1)中做出的假设,即我是F(顺便说一下,可靠的形式系统是指只有有效论证才能被证明的系统)。但是(3)"我知道G(F')是真的,其中这是系统F'的哥德尔句子"(同上)。然而,(4)哥德尔第一不完备性定理表明F'无法看到哥德尔句子是真的。此外,我们可以推断(5)我就是F'(因为F'只是F加上(1)中做出的假设,即我是F),我们也可以推断我能看到哥德尔句子的真实性(因此既然我们是F',F'能看到哥德尔句子的真实性)。也就是说,(6)我们得到了一个矛盾(F'既能看到哥德尔句子的真实性,又不能看到哥德尔句子的真实性)。因此,(7)我们的初始假设必须是错误的,也就是说,F或任何形式系统都无法捕获我的推理能力。
作为一个计算主义者,我同意(1)——至少如果所考虑的"形式系统"足够面向物理,能够潜在地包括基于物理定律对物理大脑状态的操作,就像我们在上面的例子中看到的那样。
许多批评者反对(2),如果我们认为人类的口头陈述是由形式系统产生的,我可能也反对。但当我们考虑一个以物理为导向的形式系统,其唯一公理是宇宙的初始条件,其唯一更新规则是移动到宇宙的其他状态时,我不明白我们如何能得到矛盾。事实上,我不确定在这种情况下真值意味着什么。一个宇宙状态如何成为另一个状态的否定?
但在这种情况下,哥德尔定理甚至不适用,因为形式系统无法进行算术?事实上,这个形式系统更像是一个有限状态自动机,只是依次移动到下一个状态。
我的第三个回应
我对如何将图灵机视为形式系统感到困惑。我在Quora上开始了一个讨论并提供了我自己的答案,但我仍然不理解我们如何从一个通用图灵机得到一个算术定理证明器。
从Lucas和Penrose受到的关注来看,似乎确实存在一种方式(我目前还不清楚)可以将任何图灵机视为受哥德尔定理约束的形式系统。否则这些作者就只是在驳斥人脑是一个狭义的GOFAI定理证明系统的说法,这基本上没有认知科学家相信。